

This document describes in detail the latest deterministic random number generator (RNG) algorithm used in CryptoSys API and CryptoSys PKI [updated 2024-01-03].
The RNG has been implemented to conform to NIST Special Publication 800-90A† Recommendation for Random Number Generation Using Deterministic Random Bit Generators [SP80090A]. Entropy is accumulated in "Fortuna" pools as described in Ferguson and Schneier, Practical Cryptography, chapter 10, "Generating Randomness" [FERG03].
† Note 2013-09-21: Our implementation does not use the Dual EC_DRBG component of NIST 800-90 which allegedly contains an NSA backdoor (this has anyway been removed from SP800-90A in Revision 1, June 2015).
This information is published for peer review and comment. Please send us a message.
We use the term RNG in this document to mean a cryptographically-secure PRNG, deterministic RNG or deterministic RBG (DRBG). All these terms mean the same thing for our purposes.
RNG ≡ RBG ≡ DRBG ≡ PRNG
In particular, the terms random number generator (RNG) and random bit generator (RBG) are interchangeable. The output from a RNG or RBG is a sequence of zero and one bits. In our case, the output is always in 8-bit blocks (bytes, octets).
Our objective for our RNG is to produce, on request, a sequence of the required number of random bits. The RNG should be in compliance with FIPS 140-2 and NIST SP800-90, and any issues must be documented. The RNG must be compatible with a general-purpose cryptographic library which must be usable on any 32-bit variant of the Windows® operating system in a thread-safe manner. It must not interfere with the operation of the library unless it fatally fails.
We use two basic references for the background theory: NIST Special Publication 800-90A Recommendation for Random Number Generation Using Deterministic Random Bit Generators [SP80090A] and Ferguson and Schneier, Practical Cryptography, chapter 10, "Generating Randomness" [FERG03]. Ferguson and Schneier is much easier to read and we have drawn on several sections of their book here (because they can write about the subject much better than we can).
In broad terms, there are three levels of PRNG.
A statistically-random PRNG is not necessarily cryptographically-secure. The concept of security strength is an attempt to quantify just how cryptographically secure it is.
PRNGs work by keeping an internal state. Typically this is a seed and a key, which are kept secret. When a consumer requests random data, a cryptographic algorithm operates on the seed and the key to produce pseudo-random output. The internal state is then updated so that the next request does not produce the same data. Ferguson and Schneier [FERG03] describe a simple generator using AES-256 and a 128-bit counter. NIST SP800-90A [SP80090A] specifies a whole smorgasbord of generators using message digest hashes, HMACS, block ciphers and even elliptic curves. The idea is that designers can use whichever cryptographic function is already available to them.
Some typical pseudo-code for a PRNG generator might be:
INPUT: (Key, Seed) OUTPUT: random_data, (Key', Seed') random_data = F(Key, Seed) Key' = F(Key, Seed+1) Seed' = F(Key', Seed) return random_data
where F is a cryptographic function. All the generators are essentially some variant of this.
NIST SP800-90A formalises the resistance to attacks with the concepts of Backtracking Resistance and Prediction Resistance. (In the following, remember that PRNG, RBG and DRBG all mean the same thing.)
Backtracking resistance is provided by ensuring that the DRBG generator algorithm is a one-way function. This is easy: all the DRBG mechanisms in NIST SP800-90A provide backtracking resistance.
Prediction resistance depends on the Reseed process; that is, the ability to effectively reseed after a compromise but before the next request. This is more difficult.
Source: [FERG03]
- The attacker attempts to reconstruct the internal state from the output. This is a classic cryptographic attack, and rather easy to counter using cryptographic techniques.
- The attacker is at some point able to acquire the internal state. If no further entropy is added, then the attacker can follow all the outputs and all the updates of the internal state. This means that if the the PRNG is ever attacked successfully, then it can never recover to a secure state.
To solve: mix in entropy from truly-random events into the internal state.
- If the entropy added is only in small amounts - as it most likely will be - the attacker makes frequent requests for random data from the PRNG. As long as the total amount of entropy added between two such requests is limited to say, 30 bits, then the attacker can simply try all possibilities for the random inputs and recover the new state after the mixing.
The best defence against this particular attack is to pool the incoming events that contain entropy. You collect entropy until you have enough to mix into the internal state without the attacker being able to guess the pooled data. How much is enough? You want to have 128 bits of entropy. But here is the real problem: making any kind of estimate of the amount of entropy is extremely difficult, if not impossible. It depends heavily on how much the attacker knows or can know, but that information is not available to the developers during the design phase.
Source: [FERG03]
To reseed the generator, we need to pool events in a pool large enough that the attacker can no longer enumerate the possible values for the events in the pool. Fortuna solves the problem of how many events to collect in a pool before using it to reseed the generator.
There are 32 pools: P0,P1,...,P31. Each pool conceptually contains a string of bytes of unbounded length but in practice contains the partly-computed hash of the string as it is assembled in the pool.
Each source distributes its random events over the pools in a cyclical fashion. This ensures that the entropy from each source is distributed more or less evenly over the pools. Each random event is appended to the string in the pool in question.
We reseed the generator every time pool P0 is long enough. Reseeds are numbered 1,2,3,.... Depending on the reseed number r, one or more pools are included in the reseed. Pool Pi is included if 2i is a divisor of r. Thus P0 is used in every reseed, P1 every other reseed, P2 every fourth reseed, etc. After a pool is used in a reseed, it is reset to the empty string.
Irrespective of how many fake random events the attacker generates, or how many of the events he knows, as long as there is at least one source of random events he can't predict, there will always be a pool that collects enough entropy to defeat him.
To prevent the attacker injecting so many events that even if pool P31 does not contain enough randomness between reseeds to recover from a compromise, we limit the speed of the reseeds. A reseed will only be performed if the previous reseed was more than 100 milliseconds ago, so it will take more than 13 years before P32 would have been used, had it existed.
Source: [FERG03]
The measure of randomness is called entropy. Entropy measures how uncertain you are about the value. You can think of entropy as the average number of bits you would need to specify the value if you could use an ideal compression algorithm. The more you know about a value, the smaller its entropy is.
Mathematically, the definition of entropy, H(X), for a random variable X is
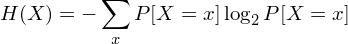
where P[X=x] is the probability that the variable X takes on the value x. See †† below for an alternative formula.
For example, if you have a value consisting of a sequence of 16 bytes that are completely random; that is, each of the sequence of 128 bits (16 bytes x 8 bits/byte = 128 bits) has been chosen in an unbiased manner, then the 16-byte value has 128 bits of entropy. You would say that the security strength of the value is 128 bits, or the amount of work required to break the security is 2128 operations. This is computationally infeasable. (The hard part, of course, is to select the bytes in an unbiased manner.)
But if you know that each byte has been chosen from the set of, say, the two values {0x00, 0xFF} (so the sequence is made up of bytes that are either 0x00 or 0xFF in some random order), then you only have 16 bits of entropy. Each byte in the sequence has entropy of only 1 bit, so the sequence has 16 bits. Thus the work required to break the security has been reduced to 216 operations: a mere 65,000 guesses.
At the far extreme, if an attacker knows exactly what these 16 bytes are, then you have zero bits of entropy.
So the amount of entropy can be anything between zero and the actual size of the value in bits depending on how much the attacker knows. It's relative to an observer and his knowledge prior to an observation.
†† A alternative formula for entropy is as follows. For a distribution with n possible outcomes with probability p1, p2, ..., pn the entropy
. For the examples above, first consider a sequence of 128 bits each randomly chosen with equal probability from {0,1}. We have n = 2128 possible outcomes each with probability p = 1/n. Substituting these values into the formula we obtain
, the number of bits we started with. Now consider the case of a sequence of 16 bytes each chosen randomly only from 0x00 or 0xFF. We have n = 216 possible outcomes, each with probability p = 1/n. This gives entropy H = 16. In other words, the sequence of 128 bits can be encoded (i.e. uniquely represented) by a bitstring of just 16 bits. This means the workload for an attacker to brute-force guess the correct answer comes down from 2128 (effectively impossible) to 216 (easy). Finally consider the case where an attacker knows exactly what the outcome is. There is only one possible outcome n = 1 with probability p = 1, and the formula gives H = log 1 = 0, i.e. zero entropy.
From FIPS PUB 140-2 Annex C Approved Random Number Generators for FIPS PUB 140-2 [FIPS140XC], January 24, 2007:
ANNEX C: APPROVED RANDOM NUMBER GENERATORS
Annex C provides a list of the FIPS Approved random number generators applicable to FIPS PUB 140-2
(snip)...
6. National Institute of Standards and Technology, Recommendation for Random Number Generation Using Deterministic Random Bit Generators, Special Publication 800-90, June 2006.
From FIPS PUB 140-2 Section 4.9.2 Self-Tests - Conditional Tests [FIPS140]:
Continuous random number generator test.
If a cryptographic module employs Approved or non-Approved RNGs in an Approved mode of operation, the module shall perform the following continuous random number generator test on each RNG that tests for failure to a constant value.
1. If each call to a RNG produces blocks of n bits (where n > 15), the first n-bit block generated after power-up, initialization, or reset shall not be used, but shall be saved for comparison with the next n-bit block to be generated. Each subsequent generation of an n-bit block shall be compared with the previously generated block. The test shall fail if any two compared n-bit blocks are equal.
Our PRNG functions use the HMAC_DRBG mechanism
as specified in Section 10.1.2 of NIST SP800-90A with SHA-512 as the underlying hash function (updated from SHA-1 in December 2023/January 2024).
Highest supported security strength = 256 Output block length (outlen) = 512 bits Maximum number of bits per request = 2^19 bits (i.e. 65536 bytes) Reseed interval = 2^30 (< 2^48 max for HMAC_DRBG) or as dictated by the Fortuna algorithm Maximum length of personalization string = 512 bits Maximum length of entropy input = 16384 bits (32 pools x 512 bits) Maximum additional input length = 2^34 bits (2^31 bytes)
Each thread has its own Generator in Thread Local Storage. Each process has one Accumulator accessed by all Generators and protected by a Critical Section when accessed. The accumulator has 32 "Fortuna" accumulation pools with the minimum pool size before a reseed set to 32 bytes.
The "personalization string" used on instantiation is formed from a hash of the user's name, computer name, volume serial number, and the values of a selection of environment variables. The instantiation nonce is a 128-bit value consisting of a 64-bit representation of the current time, the process ID, and a counter, which is incremented on the instantiation of any new Generator in a different thread.
The random events polled by the accumulator include the system time, the clock count, the memory status, the free disk space, and other system parameters expected to change during the course of the program. If Intel(R) DRNG is available, then a fresh RDSEED/RDRAND value is obtained and added to the pools. Every event is time-stamped to the accuracy of the system clock, which means that, in the worst case, we have a cumulative hash of the times of every event polled since power up.
In the absolute worst case, if no seed file is used, and Intel(R) DRNG is not available, and an attacker can call the
GenerateRandomData function before any entropy has been generated by the system,
the output is effectively a "strong" hash of the current time, PID,
personalization string and nonce with good backtracking resistance.
This is at least equivalent to an X9.31-compliant generator.
"The Digital Random Number Generator (DRNG) is an innovative hardware approach to high-quality, high-performance entropy and random number generation. It is composed of the new Intel 64 Architecture instructions RDRAND and RDSEED and an underlying DRNG hardware implementation" [INTEL-DRNG].
If available on your system, Intel(R) DRNG will be used automatically on first use of any RNG function. It will add 256 bits of entropy using hardware-generated random values. The output is used to seed and add entropy to the generator state and Fortuna accumulation pools. It is not used directly. If RDSEED is available, it will be used in preference to RDRAND. Note that, even if an attacker can monitor the output from Intel(R) DRNG, they cannot predict the output from our generator (and if an attacker can monitor that, it is the least of your problems!).
Having Intel(R) DRNG supported on your system solves the potential problem of lack of entropy at startup. Intel(R) DRNG was not available when we first introduced our SP800-90-compliant RNG functions (back in 2007), and was not widely implemented at the time of our last major update in 2013. It is now widely supported in most Intel(R) processors.
We do not make available to the consumer either a reseed_required_flag
or a prediction_resistance_request.
This is by design to prevent a clash with the Fortuna accumulation system.
Reseeds are carried out when either:
The Fortuna algorithm will reseed every time pool P0 is long enough (in our case, when its length is 32 bytes or more) AND the time-since-last-reseed is greater than 100 milliseconds. This is not directly under the consumer's control, although he can force it eventually by repeatedly calling the library functions known to trigger entropy accumulation.
The NIST DRBG mechanism reseeds on either (a) first use; or (b) at the end of the seed life. The seed life of the DRBG mechanism is deliberately set high to reduce the risk of an attacker forcing a reseed by repeatedly requesting random data.
If the DRBG mechanism requires a reseed, then it requests entropy from the Fortuna pools, which is provided unconditionally.
A random number generator Health Check is carried out on power up and every time a new RNG generator is instantiated in a new thread. It can also be carried out on demand. The health check performs self-tests to obtain assurance that the DRBG continues to operate as designed and implemented according to section 11.3 of [SP80090A] including Known Answer Testing, Testing the Instantiate Function, Testing the Generate Function, Testing the Reseed Function and Testing the Uninstantiate Function.
We use a 64-bit value for continuous checks as required in Section 4.9.2 of FIPS 140-2. Every time the consumer requests a set of random data, we generate an extra 64-bit value which is not output but is stored for comparison purposes. If this matches the first 64 bits of the next about-to-be-output data, then we throw a catastrophic error. If the length of the requested random data is less than 64 bits, then we pad the about-to-be-output data to 64 bits with zeroes before comparison. On start-up, we generate a 64-bit block that is not used for output but is saved for comparison with the next request.
In pseudo-code:
INPUT: nbits, previous_block
OUTPUT: random_data, previous_block'
if (previous_block != Null)
{
random_data = GenerateRandomData(nbits)
if (nbits < 64)
tocompare = random_data || 0^(64 - nbits)
else
tocompare = LeftMostBits(random_data, 64)
if (tocompare == previous_block)
return "catastrophic error"
}
previous_block' = GenerateRandomData(64)
return random_data
A strict reading of FIPS 140-2 would seem to require a check of every successive 64-bit block generated
by the DRBG_Generate function where the requested number of bits is greater than 64.
We assert that this pointless unless the HMAC function is corrupted.
Furthermore, and far more serious, storing every generated block to compare with the next would expose a huge
security hole.
We chose the HMAC_DRBG mechanism because:
HMAC_DRBG is preferred to Hash_DRBG because it is more secure.
There are known problems with
Hash_DRBG when the DRBG is instantiated with insufficient entropy for the requested
security strength.
But HMAC outputs look random even given knowledge and control over the inputs when an attacker doesn't know the key used.
Ref: [SP80090A] Appendix C.2. (In other words, you won't be able to tell if we get it wrong.)
We can see at least the one potential problem. We'd be happy to discuss them if you have some constructive comments.
However, if Intel(R) DRNG is available then this solves this issue.
Actually, we don't do any of this. We just use the stdlib rand() function. Here is the source code.
We know nobody ever reads this far :-)
#include <stdlib.h>
#include <time.h>
void rng_bytes(unsigned char *buf, int nbytes)
{
static unsigned int seed;
int i;
if (seed == 0) {
seed = ((unsigned)time(NULL) << 16) ^ (unsigned)clock();
srand(seed);
}
for (i = 0; i < nbytes; i++)
buf[i] = rand() & 0xFF;
}
For more information or to comment on this page, please send us a message.
This page last updated 10 September 2025.